z arkusza... Nadia: Oto zadanie które powinnam rozwiązać, jednak nie wiem z której strony się do niego zabrać Bardzo proszę o jakieś wskazówki co mam zrobić w jakiej kolejności... Punkty A=(1,3), C= (7,1) są przeciwległymi wierzchołkami kwadratu ABCD. Wyznacz współrzędne pozostałych wierzchołków tego kwadratu.

AROB: pomagam

AROB: Już piszę, bo miałam małą przeszkodę.

Nadia: ok, i tak się bardzo cieszę że pojawiła się dla mnie jakaś iskierka nadziei ^^

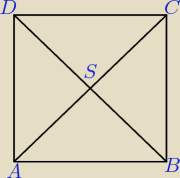
AROB: Dane: A(1,3), C(7,1) B,D = ? − Wyznaczam współrzędne punktu przecięcia przekątnych (S).

	xA + xC		1+7
S(xS,yS), xS =		=		= 4
	2		2

	yA + yC		3+1
yS =		=		= 2, czyli S(4,2)
	2		2

	yC−yA		1−3		1
− Współczynnik kier. prostej AC; aAC =		=		= −
	xC−xA		7−1		3

	1
Zatem aBD = −		= 3
	aAC

−Wyznaczam równanie prostej BD: y− y_S = a_BD (x − x_S) y − 2 = 3(x − 4) ⇒ y = 3x − 10 Stąd: punkt B∊ BD, czyli y_B = 3x_b − 10. − Obliczam dług. Przekątnej AC: IACI − √(x_C−x_A)² + (y_c−y_A)² = = √(7−1)² + (1−3)² = √40 = 2√10.

	1
− IBDI =IACI = 2√10 ⇒ ISBI =		IBDI = √10
	2

−Ze wzoru na długość ISBI wyznaczę współrzędne szukanych puktów. ISBI = √(x_B − x_S)² + (y_B − y_S)² √(x_B − 4)² + (y_B − 2)² = √10 Podnosimy obustronnie do kwadratu. (x_B−4)² + (3x_B −10−2)² = 10 x_B²−8x_B + 16 + (3x_B − 12)² = 10 x_B² − 8x_B + 16 + 9x_B² − 72x_B +144 − 10 = 0 10x_B² − 80x_B + 150 = 0 /:10 x_B² −8x_B + 15 = 0 ⇒ Δ = 4, √Δ = 2, X_B = 5 lub x_B = 3 Zatem dla x_B=5, y_B = 5, a dla x_B = 3, y_B = −1 Odp. B(3, −1), D(5, 5)

Nadia: AROB− dzięki wielkie za tak dokładne rozwiązanie! Teraz jak na to teraz patrzę to faktycznie jest to do zrobienia. Przeanalizuję sobie i spróbuję rozwiązać sama bez patrzenia na rozwiązanie. Jeszcze raz dziękuję!

AROB: Powodzenia!

AROB: Dobrej nocy ABBA i pozostali wytrwali. Do jutra!